Časovno odvisna perturbacija II

Iz Kvantna Mehanika I 2006 - 2007

Revision as of 17:11, 1 junij 2007 by WikiSysop (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Naloga

Obravnavaj sistem dveh delcev s spinom $1 / 2$ s hamiltonianom

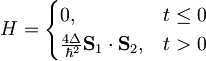
$H=\begin{cases}0,&t\leq 0\\\frac{4\Delta}{\hbar^2}\mathbf{S}_1\cdot\mathbf{S}_2,&t>0\end{cases}$

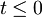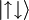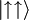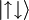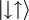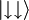
Sistem je za $t\leq0$ v stanju $\left|\uparrow\downarrow\right\rangle$ . Pošči verjetnost, da se sistem ob času $t > 0$ nahaja v stanju $\left|\uparrow\uparrow\right\rangle$ , $\left|\uparrow\downarrow\right\rangle$ , $\left|\downarrow\uparrow\right\rangle$ ali $\left|\downarrow\downarrow\right\rangle$

če problem rešiš točno.
v prvem redu perturbacije.

Pod katerimi pogoji da perturbacijska teorija pravilen rezultat?

Rešitev

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/%C4%8Casovno_odvisna_perturbacija_II«