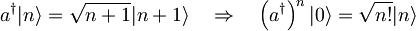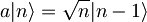Harmonski oscilator I

Iz Kvantna Mehanika I 2006 - 2007

Revision as of 23:46, 26 marec 2007 by 193.2.191.7 (Pogovor)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Skoči na: navigacija, iskanje

Vsebina

1 Naloga
2 Rešitev

Naloga

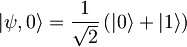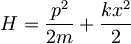Kako se s časom spreminjata pričakovani vrednosti operatorjev $x$ in $x 2$ v stanju $\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)$ harmonskega oscilatorja $H=\frac{p^2}{2m}+\frac{kx^2}{2}$ ?
Izračunaj časovno odvisnost anihilacijskega operatorja 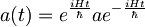$a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}$ in rezultat uporabi za izračun količin iz naloge 1.

Rešitev

Formalizem harmonskega oscilatorja

K reševanju problema harmonskega oscilatorja navadno pristopimo z uporabo/uvedbo t.i. "lestvičnih" ("ladder") operatorjev, s čimer, ob upoštevanju Diracive pisave, hitreje pridemo do vseh pomembnejših rezultatov (brez zamudnega reševanja diferencialnih enačb običajnega kvantnomehanskega formalizma).

Kreacijski in anihilacijski operator

Uvedemo anihilacijski operator a in njemu adjungiran kreacijski operator a^†:

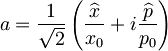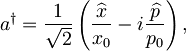
$a = \frac{1}{\sqrt{2}}\left( \frac{\widehat{x}}{x_{0}}+i \frac{\widehat{p}}{p_{0}} \right)$ in $a^{\dagger} = \frac{1}{\sqrt{2}}\left( \frac{\widehat{x}}{x_{0}}-i \frac{\widehat{p}}{p_{0}} \right) ,$

kjer sta:

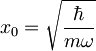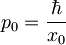$x_{0} = \sqrt{\frac{\hbar}{m \omega}}$ in $p_{0} = \frac{\hbar}{x_{0}}$ , pri čemer je frekvenca harmonskega oscilatorja: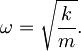 $\omega = \sqrt{\frac{k}{m}}.$

Lastnosti

$\left[ a,a^{\dagger} \right] = 1.$
$a^{\dagger}|n\rangle = \sqrt{n+1}|n+1\rangle \quad \Rightarrow \quad \left(a^{\dagger}\right)^{n}|0\rangle = \sqrt{n!}|n\rangle$
$a|n\rangle = \sqrt{n}|n-1\rangle$
$a|0\rangle = 0$

Kreacijski operator torej zvišuje stanje harmonskega oscilatorja, medtem, ko nam anihilacijski operator stanje znižuje. Pri delovanju anihilacijskega operatorja na lastno valovno funkcijo osnovenega stanja, pa jo ta izniči.

Hamiltonov operator

S tako definiranima operatorjema na novo zapišemo še Hamiltonov operator:

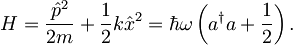
$H = \frac{\hat{p}^{2}}{2m}+\frac{1}{2}k\hat{x}^{2}=\hbar \omega \left( a^{\dagger}a+\frac{1}{2} \right).$

Lastne energije harmonskega oscilatorja v stanju n so:

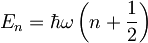$E_{n} = \hbar \omega \left( n + \frac{1}{2} \right)$ , kjer med n - to lastno energijo in Hamiltonovim operatorjem velja zveza: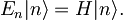 $E_{n} | n \rangle = H | n \rangle.$

Operatorja kraja in gibalne količine

Operatorja kraja 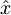$\hat{x}$ in gibalne količine 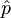$\hat{p}$ , sta sebi adjungirana oz. hermitska, na novo pa ju z anihilacijskim in kreacijskim operatorjem zapišemo v obliki:

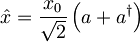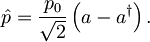
$\hat{x} = \frac{x_{0}}{\sqrt{2}}\left( a + a^{\dagger} \right)$ in $\hat{p} = \frac{p_{0}}{\sqrt{2}}\left( a - a^{\dagger} \right).$

Časovna odvisnost pričakovane vrednosti x in njegovega kvadrata

Nalogo bomo reševali na dva načina, in sicer:

V prvem primeru bomo računali pričakovano vrednost ustreznega operatorja tako, da bomo v času razvili valovno funkcijo in nato z njo delovali na operator. Za splošen operator torej računamo takole:
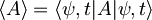
$\langle A \rangle = \langle \psi , t | A | \psi , t \rangle$
V drugem primeru bomo računali pričakovano vrednost ustreznega operatorja tako, da ga bomo najprej razvili v času in nato nanj delovali z stacionarno valovno funkcijo. Za splošen operator torej računamo takole:
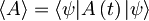
$\langle A \rangle = \langle \psi | A \left( t \right) | \psi \rangle$

Časovni razvoj valovne funkcije

Ob t=0 imamo harmonski oscilator v stanju z valovno funkcijo:

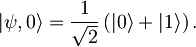
$|\psi,0\rangle = \frac{1}{\sqrt{2}}\left( |0\rangle + |1\rangle \right).$

Časovni razvoj valovne funkcije je:

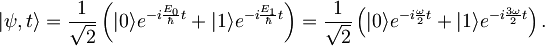
$|\psi,t\rangle = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{E_{0}}{\hbar}t} + |1\rangle e^{-i\frac{E_{1}}{\hbar}t} \right) = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{\omega}{2}t} + |1\rangle e^{-i\frac{3\omega}{2}t} \right) .$

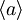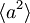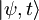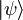Uporabimo sedaj časovni razvoj valovne funkcije za izračun $\langle a \rangle$ in $\langle a^{2} \rangle$ . Pri tem bomo za $|\psi,t\rangle$ pisali kar $|\psi\rangle$ .

Časovna odvisnost pričakovane vrednosti x

$\begin{array}{lcl} \langle x \rangle &=&\langle \psi | \hat{x} | \psi \rangle = \langle \psi | \frac{x_{0}}{\sqrt{2}}\left( a + a^{\dagger} \right) | \psi \rangle = \frac{x_{0}}{\sqrt{2}} \left( \langle a \rangle + \langle a \rangle^{\ast} \right) = \frac{x_{0}}{\sqrt{2}}2\textrm{Re}\langle a \rangle = \sqrt{2} x_{0} \textrm{Re} \langle \psi | a | \psi \rangle = \\ &=& \sqrt{2} x_{0} \textrm{Re}\left( \frac{1}{\sqrt{2}} \left[ \langle 0| e^{i\frac{\omega}{2}t} + \langle 1| e^{i\frac{3\omega}{2}t} \right] a \left[ |0\rangle e^{-i\frac{\omega}{2}t} + |1\rangle e^{-i\frac{3\omega}{2}t} \right] \frac{1}{\sqrt{2}} \right) = \sqrt{2} x_{0} \textrm{Re}\left( \frac{1}{2} \langle 0| e^{i\frac{\omega}{2}t} \sqrt{1} |0\rangle e^{-i\frac{3\omega}{2}t} \right) = \\ &=& \frac{1}{\sqrt{2}} x_{0} \cos\left( \omega t \right) \end{array}$

VRSTICA: Tu smo najprej namesto operatorja kraja vstavili njegov zapis z kreacijskim in anihilacijskim operatorjem, nato pa upoštevali distributivnost skalarnega produkta v Hilbertovem prostoru. Nazadnje smo upoštevali še, da je kreacijski operator adjungiran anihilacijskemu, od koder sledi, da je njegova pričakovana vrednost enaka konjugirani pričakovani vrednosti anihilacijskega operatorja.
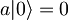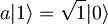VRSTICA: Bra in ket razpišemo z baznimi valovnimi funkcijami. Nato z anihilacijskim operatorjem delujemo na ket, kjer upoštevamo $a|0\rangle = 0$ in $a|1\rangle = \sqrt{1} |0\rangle$ . Nato upoštevamo še 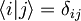$\langle i|j \rangle = \delta_{ij}$ . Ostanemo s konstantami in realnim delom časovnega razvoja valovne funkcije.

Časovna odvisnost pričakovane vrednosti kvadrata x

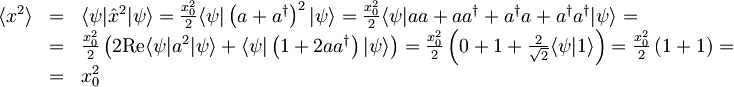
$\begin{array}{lcl} \langle x^{2} \rangle &=&\langle \psi | \hat{x}^{2} | \psi \rangle = \frac{x_{0}^{2}}{2} \langle \psi | \left( a + a^{\dagger} \right)^{2} | \psi \rangle = \frac{x_{0}^{2}}{2} \langle \psi | aa + aa^{\dagger} + a^{\dagger}a + a^{\dagger}a^{\dagger} | \psi \rangle = \\ &=& \frac{x_{0}^{2}}{2} \left( 2\textrm{Re} \langle \psi | a^{2} | \psi \rangle + \langle \psi | \left( 1+2aa^{\dagger} \right) | \psi \rangle \right) = \frac{x_{0}^{2}}{2} \left( 0+1+\frac{2}{\sqrt{2}} \langle \psi | 1 \rangle \right) = \frac{x_{0}^{2}}{2} \left( 1+1 \right) = \\ &=& x_{0}^{2} \end{array}$

VRSTICA: Najprej namesto kvadrata operatorja kraja, operator zapišemo z uporabo kreacijskega in anihilacijskega operatorja, nato izraz razpišemo.
VRSTICA:
1. Tu skalarni produkt najprej razbijemo na dva dela:
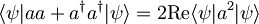  1. Velja: $\langle \psi | aa + a^{\dagger}a^{\dagger} | \psi \rangle = 2 \textrm{Re} \langle \psi | a^{2} | \psi \rangle$ , saj velja 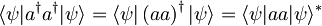$\langle \psi | a^{\dagger}a^{\dagger} | \psi \rangle = \langle \psi | \left( aa \right)^{\dagger} | \psi \rangle = \langle \psi | aa | \psi \rangle^{\ast}$ in se zato imaginarni deli odštejejo.
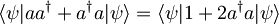  2. Velja: $\langle \psi | aa^{\dagger} + a^{\dagger}a | \psi \rangle = \langle \psi | 1+2a^{\dagger}a | \psi \rangle$ , kjer smo uporabili: $\left[ a,a^{\dagger} \right] = 1 = aa^{\dagger}-a^{\dagger}a \quad \Rightarrow \quad aa^{\dagger}+a^{\dagger}a = 1+2a^{\dagger}a$
2. Nato upoštevamo, da velja:
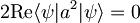  1. $2 \textrm{Re} \langle \psi | a^{2} | \psi \rangle = 0$ , ker velja 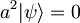$a^{2}|\psi\rangle = 0$ , saj z anihilacijskim operatorjem dvakrat delujemo na valovno funkcijo oblike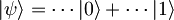 $|\psi \rangle = \cdots |0 \rangle + \cdots |1 \rangle$
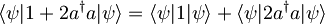  2. $\langle \psi | 1+2a^{\dagger}a | \psi \rangle = \langle \psi | 1| \psi \rangle+ \langle \psi |2a^{\dagger}a | \psi \rangle$ , kjer velja: 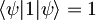$\langle \psi | 1| \psi \rangle=1$ , saj je valovna funkcija $ψ$ normirana. V drugem delu velja: 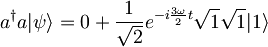$a^{\dagger}a| \psi \rangle = 0 + \frac{1}{\sqrt{2}}e^{-i\frac{3\omega}{2}t}\sqrt{1}\sqrt{1}|1\rangle$ , tako, da dobimo $\langle \psi |2a^{\dagger}a | \psi \rangle = \frac{2}{\sqrt{2}} \left[ \langle 0| e^{i\frac{\omega}{2}t} + \langle 1| e^{i\frac{3\omega}{2}t} \right] \frac{1}{\sqrt{2}} \left[ e^{-i\frac{3\omega}{2}t}|1\rangle \right] =\frac{2}{\sqrt{2}} \langle \psi | 1 \rangle = 1$ , kjer upoštevamo še $\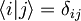langle i | j \rangle = \delta_{ij}$

Časovna odvisnost anihilacijskega operatorja

Časovni razvoj in Hamiltonov operator

Pokažimo najprej, da valovno funkcijo, s pomočjo Hamiltonovega operatorja, razvijemo v času kot:

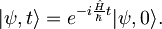
$|\psi , t \rangle=e^{-i\frac{\hat{H}}{\hbar}t}|\psi , 0 \rangle .$

Začnemo z izrazom 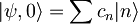$|\psi , 0 \rangle = \sum c_{n} |n\rangle$ , ki ga razvijemo v času z uporabo gornjega izraza:

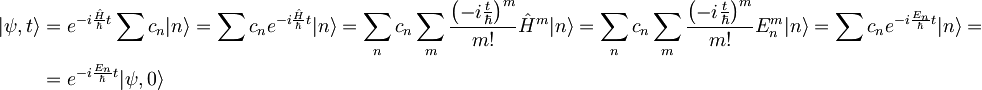
$\begin{align} |\psi , t \rangle &= e^{-i\frac{\hat{H}}{\hbar}t} \sum c_{n} |n\rangle = \sum c_{n} e^{-i\frac{\hat{H}}{\hbar}t} |n\rangle = \sum_{n} c_{n} \sum_{m} \frac{\left( -i\frac{t}{\hbar} \right)^{m}}{m!}\hat{H}^{m}|n\rangle = \sum_{n} c_{n} \sum_{m} \frac{\left( -i\frac{t}{\hbar} \right)^{m}}{m!}E_{n}^{m}|n\rangle = \sum c_{n} e^{-i\frac{E_{n}}{\hbar}t} |n\rangle = \\ &= e^{-i\frac{E_{n}}{\hbar}t} |\psi , 0 \rangle \end{align}$

V računu smo eksponentni del najprej razvili v potenčno vrsto, upoštevali zvezo 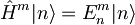$\hat{H}^{m}|n \rangle = E_{n}^{m}|n \rangle$ , nato pa vrsto spet izrazili v funkcijski obliki.

Izračun časovne odvisnosti

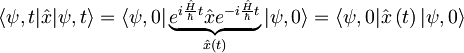
$\begin{align} \langle \psi , t| \hat{x} |\psi , t \rangle &= \langle \psi , 0| \underbrace{e^{i\frac{\hat{H}}{\hbar}t}\hat{x}e^{-i\frac{\hat{H}}{\hbar}t}}_{\hat{x}\left( t \right)} |\psi , 0 \rangle = \langle \psi , 0| \hat{x}\left( t \right) |\psi , 0 \rangle \end{align}$

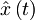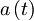Podobno, kot smo definirali $\hat{x}\left( t \right)$ , definiramo $a\left( t \right)$ :

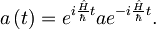
$a\left( t \right) = e^{i\frac{\hat{H}}{\hbar}t}ae^{-i\frac{\hat{H}}{\hbar}t} .$

Izraz odvajamo in dobimo:

$\begin{align} \dot{a}\left( t \right) &= \frac{i}{\hbar}\underbrace{\hat{H}e^{i\frac{\hat{H}}{\hbar}t}}_{=e^{i\frac{\hat{H}}{\hbar}t}\hat{H}}ae^{-i\frac{\hat{H}}{\hbar}t}+e^{i\frac{\hat{H}}{\hbar}t}\underbrace{\frac{\partial a}{\partial t}}_{=0}e^{-i\frac{\hat{H}}{\hbar}t}-e^{i\frac{\hat{H}}{\hbar}t}a\frac{i}{\hbar}\hat{H}e^{-i\frac{\hat{H}}{\hbar}t} = \frac{i}{\hbar}e^{i\frac{\hat{H}}{\hbar}t}\left[ \hat{H},a \right]e^{-i\frac{\hat{H}}{\hbar}t} = \\ &= \frac{i}{\hbar} \left( \underbrace{e^{i\frac{\hat{H}}{\hbar}t}\hat{H}e^{-i\frac{\hat{H}}{\hbar}t}}_{=\hat{H}}\underbrace{e^{i\frac{\hat{H}}{\hbar}t} a e^{-i\frac{\hat{H}}{\hbar}t}}_{=a\left( t \right)} - \underbrace{e^{i\frac{\hat{H}}{\hbar}t} a e^{-i\frac{\hat{H}}{\hbar}t}}_{=a\left( t \right)}\underbrace{e^{i\frac{\hat{H}}{\hbar}t}\hat{H}e^{-i\frac{\hat{H}}{\hbar}t}}_{=\hat{H}} \right) = \\ &= \frac{i}{\hbar} \left[ \hat{H},a\left( t \right) \right] \end{align}$

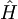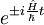V računu smo upoštevali, da operatorja $\hat{H}$ in $e^{\pm i\frac{\hat{H}}{\hbar}t}$ komutirata, tako, da velja:

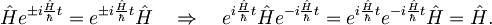
$\hat{H}e^{\pm i\frac{\hat{H}}{\hbar}t} = e^{\pm i\frac{\hat{H}}{\hbar}t}\hat{H} \quad \Rightarrow \quad e^{i\frac{\hat{H}}{\hbar}t}\hat{H}e^{-i\frac{\hat{H}}{\hbar}t} = e^{i\frac{\hat{H}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\hat{H} = \hat{H} .$

Preden nadaljujemo z izračunom, si za poljubna operatorja A in B poglejmo še nekaj lastnosti časovnega razvoja operatorjev:

$\dot{A}\left( t \right) = \frac{i}{\hbar} \left[ \hat{H},A\left( t \right) \right] + \left( \frac{\partial A}{\partial t} \right) \left( t \right)$
Pokažimo, da velja zveza: $\left[ \hat{H},A \right] \left( t \right) = \left[ \hat{H} \left( t \right),A \left( t \right) \right]$ $\begin{align} \left[ \hat{H},A \right] \left( t \right) &= e^{i\frac{\hat{H}}{\hbar}t} \left[ \hat{H},A \right] e^{-i\frac{\hat{H}}{\hbar}t} = e^{i\frac{\hat{H}}{\hbar}t} \left( \hat{H}A - A \hat{H} \right) e^{-i\frac{\hat{H}}{\hbar}t} = e^{i\frac{\hat{H}}{\hbar}t} \hat{H}A e^{-i\frac{\hat{H}}{\hbar}t} - e^{i\frac{\hat{H}}{\hbar}t} A \hat{H} e^{-i\frac{\hat{H}}{\hbar}t} = \\ &= \underbrace{e^{i\frac{\hat{H}}{\hbar}t} \hat{H} e^{-i\frac{\hat{H}}{\hbar}t}}_{=\hat{H}\left( t \right)} \underbrace{e^{i\frac{\hat{H}}{\hbar}t} A e^{-i\frac{\hat{H}}{\hbar}t}}_{=A\left( t \right)} - \underbrace{e^{i\frac{\hat{H}}{\hbar}t} A e^{-i\frac{\hat{H}}{\hbar}t}}_{=A\left( t \right)} \underbrace{e^{i\frac{\hat{H}}{\hbar}t}\hat{H} e^{-i\frac{\hat{H}}{\hbar}t}}_{=\hat{H}\left( t \right)} = \left[ \hat{H} \left( t \right),A \left( t \right) \right] \end{align}$
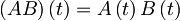
$\left( AB \right) \left( t \right) = A \left( t \right) B \left( t \right)$
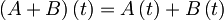
$\left( A+B \right) \left( t \right) = A \left( t \right) + B \left( t \right)$
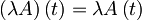
$\left( \lambda A \right) \left( t \right) = \lambda A \left( t \right)$

Nadaljujmo z izračunom časovne odvisnosti anihilacijskega operatorja:

$\dot{a}\left( t \right) = \frac{i}{\hbar} \left[ \hat{H} \left( t \right),a\left( t \right) \right] + \underbrace{\left( \frac{\partial a}{\partial t} \right) \left( t \right)}_{=0} = \frac{i}{\hbar} \left[ \hat{H},a \right] \left( t \right)$

Velja: $\begin{align} \left[ \hat{H},a \right] &= \left[ \hbar \omega \left( a^{\dagger}a + \frac{1}{2} \right) , a \right] = \hbar \omega \left( \underbrace{\left[ a^{\dagger},a \right]}_{=-1} a + a^{\dagger} \underbrace{\left[ a,a \right]}_{=0} \right) = - \hbar \omega a \end{align}$

Od tod dobimo diferencialno enačbo za anihilacijski operator, ki je oblike:

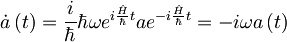
$\dot{a} \left( t \right) = \frac{i}{\hbar} \hbar \omega e^{i\frac{\hat{H}}{\hbar}t} a e^{-i\frac{\hat{H}}{\hbar}t} = -i \omega a \left( t \right)$

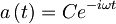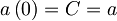Rešitev enačbe je $a \left( t \right) = C e^{-i \omega t}$ , kjer upoštevamo še: $a\left( 0 \right) = C = a$ .

Časovni razvoj anihilacijskega operatorja je torej:

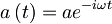$a \left( t \right) = a e^{-i \omega t}$ .

Časovna odvisnost pričakovane vrednosti x

Izračunajmo sedaj pričakovano vrednost koordinate še s časovnim razvojem anihilatorskega operatorja. Iz prvega izračuna vemo, da je 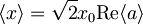$\langle x \rangle = \sqrt{2} x_{0} \textrm{Re} \langle a \rangle$ .

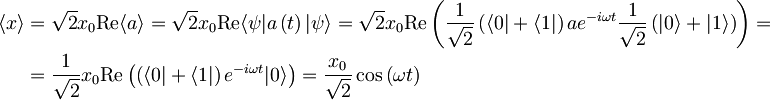
$\begin{align} \langle x \rangle &= \sqrt{2} x_{0} \textrm{Re} \langle a \rangle = \sqrt{2} x_{0} \textrm{Re} \langle \psi | a \left( t \right) | \psi \rangle = \sqrt{2} x_{0} \textrm{Re} \left( \frac{1}{\sqrt{2}} \left( \langle 0 | + \langle 1 | \right) a e^{-i \omega t} \frac{1}{\sqrt{2}} \left( | 0 \rangle + | 1 \rangle \right) \right) = \\ &= \frac{1}{\sqrt{2}} x_{0} \textrm{Re} \left( \left( \langle 0 | + \langle 1 | \right) e^{-i \omega t} | 0 \rangle \right) = \frac{x_{0}}{\sqrt{2}} \cos \left( \omega t \right) \end{align}$

Časovna odvisnost pričakovane vrednosti kvadrata x

Izračunajmo s časovnim razvojem anihilatorskega operatorja še pričakovano vrednost kvadrata koordinate . Iz prvega izračuna vemo, da je 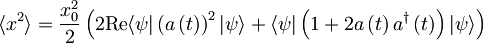$\langle x^{2} \rangle = \frac{x_{0}^{2}}{2} \left( 2\textrm{Re} \langle \psi | \left( a \left( t \right) \right)^{2} | \psi \rangle + \langle \psi | \left( 1+2a\left( t \right) a^{\dagger} \left( t \right) \right) | \psi \rangle \right)$ .

Upoštevamo naslenje zveze:

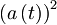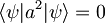Ko v enačbo vstavimo $\left( a \left( t \right) \right)^{2}$ , z enakimi argumenti, kot v prvem primeru velja: $\langle \psi | a^{2} | \psi \rangle = 0$ .
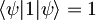Ker je valovna funkcija $ψ$ normirana, je $\langle \psi | 1| \psi \rangle = 1$ .
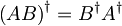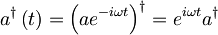Za adjungirane operatorje velja: $\left( AB \right)^{\dagger} = B^{\dagger} A^{\dagger}$ . Od tod dobimo iz časovnega razvoja anihilacijskega operatorja kreacijskega: $a^{\dagger}\left( t \right) = \left( a e^{-i \omega t} \right)^{\dagger} = e^{i \omega t} a^{\dagger}$ .

V enačbo vstavimo časovni razvoj kreacijskega operatorja, upoštevamo ostali zvezi in zveze, ki smo jih uporabili v prvem primeru ter dobimo:

$\langle x^{2} \rangle = \frac{x_{0}^{2}}{2} \left( 0 + 1 + 2 \langle \psi | \left( a \underbrace{e^{-i \omega t} e^{i \omega t}}_{=1} a^{\dagger} \right) | \psi \rangle \right) = \frac{x_{0}^{2}}{2} \left( 0 + 1 + \frac{2}{\sqrt{2}} \left[ \langle 0| + \langle 1| \right] \frac{1}{\sqrt{2}} \left[ |1\rangle \right] \right) = \frac{x_{0}^{2}}{2} \left( 0 + 1 + 1 \right) = x_{0}^{2}$ .

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Harmonski_oscilator_I«