Dvonivojski sistem I

(Primerjava redakcij)

Redakcija: 08:13, 19 september 2007

Obravnavaj delec v neskončni potencialni jami med $- a / 2$ in $a / 2$ z dodatnim potencialom 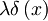$\lambda\delta\left(x\right)$ :

Pokaži, da so liha lastna stanja takega sistema enaka lihim lastnim stanjem neskončne potencialne jame.
Izpelji transcendentno enačbo za energije sodih lastnih stanj.
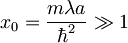Izračunaj energijo in valovno funkcijo osnovnega stanja ob predpostavki, da je $x_0=\frac{m\lambda a}{\hbar^2}\gg 1$ .
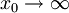Obravnavaj osnovno stanje sistema v limiti $x_0\rightarrow\infty$ .
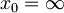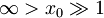Ob $t = 0$ je delec v osnovem stanju v levi polovici potencialne jame z $x_0=\infty$ . Nato potencialno bariero nekoliko znižamo, tako da velja $\infty>x_0\gg 1$ . Razvij valovno funkcijo delca po lastnih stanjih tega sistema.

 # Obravnavaj osnovno stanje sistema v limiti <math>x_0\rightarrow\infty</math>.
 # Ob <math>t=0</math> je delec v osnovem stanju v levi polovici potencialne jame z <math>x_0=\infty</math>. Nato potencialno bariero nekoliko znižamo, tako da velja <math>\infty>x_0\gg 1</math>. Razvij valovno funkcijo delca po lastnih stanjih tega sistema.
-== Rešitev ==
+== [[Media:porocilo.pdf|Rešitev]] ==