Vrtilna količina III

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)

WikiSysop (Pogovor | prispevki)
(New page: == Naloga == Obravnavaj kvantno vrtavko :<math>H=\frac{L_x^2}{2I_x}+\frac{L_y^2}{2I_y}+\frac{L_z^2}{2I_z}</math>, kjer so <math>L_x </math>, <math>L_y </math> in <math>L_z </math> kompo...)
Novejše urejanje →

Trenutna redakcija

[spremeni] Naloga

Obravnavaj kvantno vrtavko

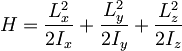$H=\frac{L_x^2}{2I_x}+\frac{L_y^2}{2I_y}+\frac{L_z^2}{2I_z}$ ,

kjer so $L x$ , $L y$ in $L z$ komponente vrtilne količine, $I x$ , $I y$ in $I z$ pa ustrezni vztrajnostni momenti.

Izračunaj lastne energije sistema za primer simetrične vrtavke ( 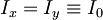$I_x=I_y\equiv I_0$ ). Vsakemu energijskemu nivoju določi degeneracijo in pripiši ustrezna kvantna števila. Namig: Izrazi Hamiltonov operator z operatorjema 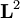$\mathbf{L}^2$ in $L z$ .
V prvem redu perturbacije obravnavaj energijske nivoje nekoliko asimetrične vrtavke:
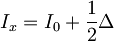$I_x=I_0+\frac{1}{2}\Delta$ ,
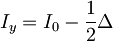$I_y=I_0-\frac{1}{2}\Delta$ ,
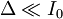$\Delta\ll I_0$ .
Dve enaki simetrični vrtavki sta sklopljeni s feromagnetno sklopitvijo
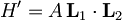$H^\prime=A\,\mathbf{L}_1\cdot\mathbf{L}_2$ ,

kjer je 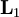$\mathbf{L}_1$ vrtilna količina prve vrtavke, 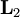$\mathbf{L}_2$ pa vrtilna količina druge vrtavke. V prvem redu perturbacije obravnavaj vpliv sklopitve na energijske nivoje z

l = 0

l = 1

[spremeni] Rešitev

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Vrtilna_koli%C4%8Dina_III«