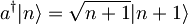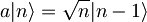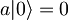Harmonski oscilator I
Iz Kvantna Mehanika I 2006 - 2007
| Redakcija: 22:26, 21 marec 2007 (spremeni) 193.2.191.7 (Pogovor) ← Pojdi na prejšnje urejanje |
Redakcija: 22:30, 21 marec 2007 (spremeni) (undo) 193.2.191.7 (Pogovor) Novejše urejanje → |
||
| Vrstica 24: | Vrstica 24: | ||
| =====Lastnosti===== | =====Lastnosti===== | ||
| - | #Komutator med anihilacijskim in kreacijskim operatorjem je: <math>\left[ a,a^{\dagger} \right] = 1.</math> | + | #<math>\left[ a,a^{\dagger} \right] = 1.</math> |
| + | #<math>a^{\dagger}|n\rangle = \sqrt{n+1}|n+1\rangle</math> | ||
| + | #<math>a|n\rangle = \sqrt{n}|n-1\rangle</math> | ||
| + | #<math>a|0\rangle = 0</math> | ||
Redakcija: 22:30, 21 marec 2007
Vsebina |
Naloga
- Kako se s časom spreminjata pričakovani vrednosti operatorjev x in x2 v stanju
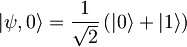 harmonskega oscilatorja
harmonskega oscilatorja 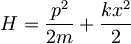 ?
?
- Izračunaj časovno odvisnost anihilacijskega operatorja
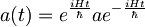 in rezultat uporabi za izračun količin iz naloge 1.
in rezultat uporabi za izračun količin iz naloge 1.
Rešitev
Formalizem harmonskega oscilatorja
K reševanju problema harmonskega oscilatorja navadno pristopimo z uporabo/uvedbo t.i. "lestvičnih" ("ladder") operatorjev, s čimer, ob upoštevanju Diracive pisave, hitreje pridemo do vseh pomembnejših rezultatov (brez zamudnega reševanja diferencialnih enačb običajnega kvantnomehanskega formalizma).
Kreacijski in anihilacijski operator
Uvedemo anihilacijski operator a in njemu adjungiran kreacijski operator a†:
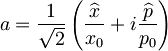 in
in 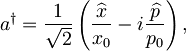
kjer sta:
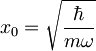 in
in 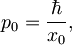 kjer je frekvenca harmonskega oscilatorja:
kjer je frekvenca harmonskega oscilatorja: 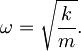
Lastnosti
Hamiltonov operator
S tako definiranima operatorjema na novo zapišemo še Hamiltonov operator:
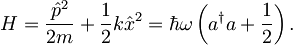
Lastne energije harmonskega oscilatorja v stanju n so:
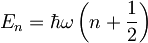 , kjer med n - to lastno energijo in Hamiltonovim operatorjem velja zveza:
, kjer med n - to lastno energijo in Hamiltonovim operatorjem velja zveza: 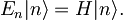
Operatorja kraja in gibalne količine
Operatorja kraja 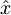 in gibalne količine
in gibalne količine 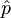 , sta sebi adjungirana oz. hermitska, na novo pa ju z anihilacijskim in kreacijskim operatorjem zapišemo v obliki:
, sta sebi adjungirana oz. hermitska, na novo pa ju z anihilacijskim in kreacijskim operatorjem zapišemo v obliki:
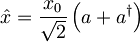 in
in 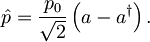
![\left[ a,a^{\dagger} \right] = 1.](/wiki/images/math/f/2/0/f20424053ecf29c90e50cc2f00a87503.png)