Dvonivojski sistem II

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)

Redakcija: 18:00, 19 marec 2007

Naloga

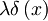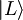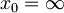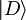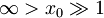Obravnavaj delec v neskončni potencialni jami med $- a / 2$ in $a / 2$ z dodatnim potencialom $\lambda\delta\left(x\right)$ . Ob $t = 0$ je delec v osnovem stanju $|L\rangle$ v levi polovici potencialne jame z $x_0=\infty$ (osnovno stanje v desni polovici potencialne jame označimo z $|D\rangle$ ). Nato potencialno bariero nekoliko znižamo, tako da velja $\infty>x_0\gg 1$ .

Izračunaj časovni razvoj valovne funkcije delca.
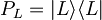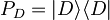Pokaži, da sta $P_L=|L\rangle\langle L|$ in $P_D=|D\rangle\langle D|$ operatorja meritve v obravnavanem dvonivojskem sistemu (za operatorje meritve velja 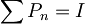$\sum P_n=I$ in $P n P m = δ n m P n$ ).
Kolikšna je verjetnost, da se po meritvi ob času $t$ delec nahaja v levem (desnem) delu potencialne jame? V kakšnem stanju je delec takoj po meritvi v vsakem od obeh primerov?
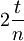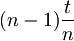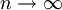Kolikšna je verjetnost, da se po meritvi ob času $t$ delec nahaja v levem (desnem) delu potencialne jame, če smo pred tem opravili enako meritev ob časih $\frac{t}{n}$ , $2\frac{t}{n}$ , ..., $(n-1)\frac{t}{n}$ , kjer gre $n\rightarrow\infty$ ?

Rešitev

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Dvonivojski_sistem_II«