Koherentna stanja harmonskega oscilatorja II
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 11:19, 26 marec 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == == Rešitev ==) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (11:28, 26 marec 2007) (spremeni) (undo) WikiSysop (Pogovor | prispevki) |
||
| Vrstica 1: | Vrstica 1: | ||
| == Naloga == | == Naloga == | ||
| + | |||
| + | Delec z nabojem <math>e</math> je v osnovnem stanju harmonskega oscilatorja <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>. Ob <math>t=0</math> v trenutku vključimo homogeno električno polje <math>E</math>. Izračunaj časovno odvisnost položaja, gibalne količine in energije delca ter nedoločenosti teh količin. Pokaži, da so pri makroskopskih nihanjih odstopanja od pričakovanih vrednosti zanemarljiva. | ||
| == Rešitev == | == Rešitev == | ||
Trenutna redakcija
[spremeni] Naloga
Delec z nabojem e je v osnovnem stanju harmonskega oscilatorja 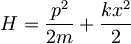 . Ob t = 0 v trenutku vključimo homogeno električno polje E. Izračunaj časovno odvisnost položaja, gibalne količine in energije delca ter nedoločenosti teh količin. Pokaži, da so pri makroskopskih nihanjih odstopanja od pričakovanih vrednosti zanemarljiva.
. Ob t = 0 v trenutku vključimo homogeno električno polje E. Izračunaj časovno odvisnost položaja, gibalne količine in energije delca ter nedoločenosti teh količin. Pokaži, da so pri makroskopskih nihanjih odstopanja od pričakovanih vrednosti zanemarljiva.