Harmonski oscilator I

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)

Redakcija: 20:20, 21 marec 2007

Naloga

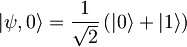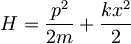Kako se s časom spreminjata pričakovani vrednosti operatorjev $x$ in $x 2$ v stanju $\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)$ harmonskega oscilatorja $H=\frac{p^2}{2m}+\frac{kx^2}{2}$ ?
Izračunaj časovno odvisnost anihilacijskega operatorja 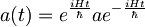$a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}$ in rezultat uporabi za izračun količin iz naloge 1.

Rešitev

Formalizem harmonskega oscilatorja

K reševanju problema harmonskega oscilatorja navadno pristopimo z uporabo/uvedbo t.i. "lestvičnih" ("ladder") operatorjev, s čimer ob upoštevanju Diracive pisave, hitro (brez zamudnega reševanja diferencialnih enačb) pridemo do vseh pomembnejših rezultatov.

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Harmonski_oscilator_I«

Redakcija: 20:08, 21 marec 2007 (spremeni) 193.2.191.7 (Pogovor) ← Pojdi na prejšnje urejanje		Redakcija: 20:20, 21 marec 2007 (spremeni) (undo) 193.2.191.7 (Pogovor) Novejše urejanje →
Vrstica 8:		Vrstica 8:
	===Formalizem harmonskega oscilatorja===		===Formalizem harmonskega oscilatorja===

-	K reševanju problema harmonskega oscilatorja navadno z uporabo/uvedbo t.i. "lestvičnih" ("ladder") operatorjev	+	K reševanju problema harmonskega oscilatorja navadno pristopimo z uporabo/uvedbo t.i. "lestvičnih" ("ladder") operatorjev, s čimer ob upoštevanju Diracive pisave, hitro (brez zamudnega reševanja diferencialnih enačb) pridemo do vseh pomembnejših rezultatov.