Harmonski oscilator I

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)
Skoči na: navigacija, iskanje
Redakcija: 18:26, 19 marec 2007 (spremeni)
WikiSysop (Pogovor | prispevki)

← Pojdi na prejšnje urejanje		 Redakcija: 19:06, 21 marec 2007 (spremeni) (undo)
193.2.191.7 (Pogovor)

Novejše urejanje →
Vrstica 5: Vrstica 5:
== Rešitev == == Rešitev ==
 +
 +===Formalizem harmonskega oscilatorja===
 +
 +V enodimenzionalnem problemu harmonskega oscilatorja obravnavamo delec z maso <math>m</math> v potencialu <math> V(x) = \frac{1}{2}kx^{2} .</math>

Redakcija: 19:06, 21 marec 2007

Naloga

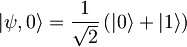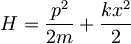  1. Kako se s časom spreminjata pričakovani vrednosti operatorjev x in x2 v stanju \left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right) harmonskega oscilatorja H=\frac{p^2}{2m}+\frac{kx^2}{2}?
  2. Izračunaj časovno odvisnost anihilacijskega operatorja 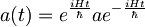a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}} in rezultat uporabi za izračun količin iz naloge 1.

Rešitev

Formalizem harmonskega oscilatorja

V enodimenzionalnem problemu harmonskega oscilatorja obravnavamo delec z maso m v potencialu V(x) = \frac{1}{2}kx^{2} .

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Harmonski_oscilator_I«