Harmonski oscilator I
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 18:23, 19 marec 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: # Kako se s časom spreminjata pričakovani vrednosti operatorjev <math>x</math> in <math>x^2</math> v stanju <math>\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\...) ← Pojdi na prejšnje urejanje |
Redakcija: 18:26, 19 marec 2007 (spremeni) (undo) WikiSysop (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 1: | Vrstica 1: | ||
| + | == Naloga == | ||
| + | |||
| # Kako se s časom spreminjata pričakovani vrednosti operatorjev <math>x</math> in <math>x^2</math> v stanju <math>\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)</math> harmonskega oscilatorja <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>? | # Kako se s časom spreminjata pričakovani vrednosti operatorjev <math>x</math> in <math>x^2</math> v stanju <math>\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)</math> harmonskega oscilatorja <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>? | ||
| # Izračunaj časovno odvisnost anihilacijskega operatorja <math>a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}</math> in rezultat uporabi za izračun količin iz naloge 1. | # Izračunaj časovno odvisnost anihilacijskega operatorja <math>a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}</math> in rezultat uporabi za izračun količin iz naloge 1. | ||
| + | |||
| + | == Rešitev == | ||
Redakcija: 18:26, 19 marec 2007
Naloga
- Kako se s časom spreminjata pričakovani vrednosti operatorjev x in x2 v stanju
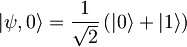harmonskega oscilatorja 
?
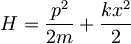- Izračunaj časovno odvisnost anihilacijskega operatorja
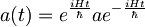in rezultat uporabi za izračun količin iz naloge 1.