Kvazivezana stanja končne potencialne jame

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)

Skoči na: navigacija, iskanje

Redakcija: 07:40, 5 marec 2007

Naloga

Za delec v končni potencialni jami širine $a$ in globine $V 0$ pokaži:

da ima amplituda za prepustnost pol pri energiji vsakega od vezanih stanj
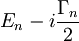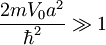da ima amplituda za prepustnost pole tudi pri energijah $E_n-i\frac{\Gamma_n}{2}$ , kjer so $E n$ in $Γ n$ energije in širine resonanc v prepustnosti (predpostavi, da velja $\frac{2mV_0a^2}{\hbar^2}\gg1$ )

Kako sta povezana razpadni čas kvazivezanega stanja in širina ustrezne resonance?

Rešitev

Pri eni izmed prejšnjih vaj smo prišli do izraza za prepustnost končne potencialne jame:

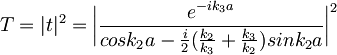
$T=|t|^2=\bigg|\frac{e^{-ik_3a}}{cosk_2a-\frac{i}{2}(\frac{k_2}{k_3}+\frac{k_3}{k_2})sink_2a}\bigg|^2$

in v bližini resonanc:

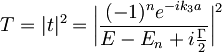
$T=|t|^2=\bigg|\frac{(-1)^ne^{-ik_3a}}{E-E_n+i\frac{\Gamma}{2}}\bigg|^2$

Zanima nas, kje imata ti amplitudi prepustnosti pole. Iz prvega izraza sledi, da mora v polih veljati:

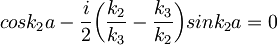
$cosk_2a-\frac{i}{2}\bigg(\frac{k_2}{k_3}-\frac{k_3}{k_2}\bigg)sink_2a=0$

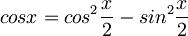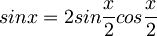
Izraza za sinus in kosinus preoblikujemo z relacijami za polovične kote: $cosx=cos^2\frac{x}{2}-sin^2\frac{x}{2}$ in $sinx=2sin\frac{x}{2}cos\frac{x}{2}$

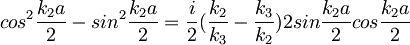
$cos^2\frac{k_2a}{2}-sin^2\frac{k_2a}{2}=\frac{i}{2}(\frac{k_2}{k_3}-\frac{k_3}{k_2})2sin\frac{k_2a}{2}cos\frac{k_2a}{2}$

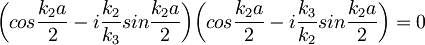
$\bigg(cos\frac{k_2a}{2}-i\frac{k_2}{k_3}sin\frac{k_2a}{2}\bigg)\bigg(cos\frac{k_2a}{2}-i\frac{k_3}{k_2}sin\frac{k_2a}{2}\bigg)=0$

Sedaj je pogoj za pol:

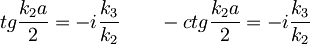
$tg\frac{k_2a}{2}=-i\frac{k_3}{k_2} \qquad -ctg\frac{k_2a}{2}=-i\frac{k_3}{k_2}$

Opazimo, da sta enačbi zelo podobni pogoju za energije vezanih stanj končne potencialne jame.

Uvedemo novo spremenljivko:

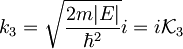$k_3=\sqrt{\frac{2m|E|}{\hbar^2}}i=i\mathcal{K}_3$ (ker E<0 pri vezanih stanjih)

In pridemo do:

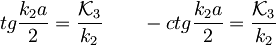
$tg\frac{k_2a}{2}=\frac{\mathcal{K}_3}{k_2} \qquad -ctg\frac{k_2a}{2}=\frac{\mathcal{K}_3}{k_2}$

Ti dve enačbi pa imata točno tako obliko kot enačbe za vezana stanja v končni potencialni jami.

To, da ima prepustnost pole tudi pri energijah 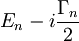$E_n-i\frac{\Gamma_n}{2}$ , sledi direktno iz druge enačbe, saj je takrat imenovalec enak nič.

Lahko pa do istega rezultata pridemo tudi na drug, daljši način.

Iščemo torej pri katerih drugih energijah bi lahko prepustnost imela še pole. Poskusimo z: $k 2 a = n π$

Vstavimo v enačbi za pole.

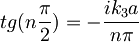$tg\big(n\frac{\pi}{2}\big)=-\frac{ik_3a}{n\pi}$ To bo res, kadar je n sod in veliko število.

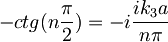$-ctg\big(n\frac{\pi}{2}\big)=-i\frac{ik_3a}{n\pi}$ To bo res, kadar je n lih in veliko število.

Nastavek: $x = k 2 a = n π + ε$

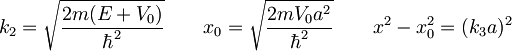
Razvijemo tangens in upoštevamo oznake, ki smo jih vpeljali pri računanju vezanih stanj končne potencialne jame $k_2=\sqrt{\frac{2m(E+V_0)}{\hbar^2}} \qquad x_0=\sqrt{\frac{2mV_0a^2}{\hbar^2}} \qquad x^2-x_0^2=(k_3a)^2$

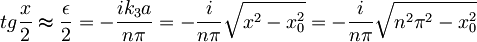
$tg\frac{x}{2}\thickapprox \frac{\epsilon}{2}=-\frac{ik_3a}{n\pi}=-\frac{i}{n\pi}\sqrt{x^2-x_0^2}=-\frac{i}{n\pi}\sqrt{n^2\pi^2-x_0^2}$

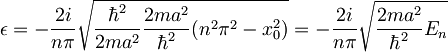
$\epsilon=-\frac{2i}{n\pi}\sqrt{\frac{\hbar^2}{2ma^2}\frac{2ma^2}{\hbar^2}(n^2\pi^2-x_0^2)}=-\frac{2i}{n\pi}\sqrt{\frac{2ma^2}{\hbar^2}E_n}$

To vstavimo v:

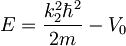
$E=\frac{k_2^2\hbar^2}{2m}-V_0$

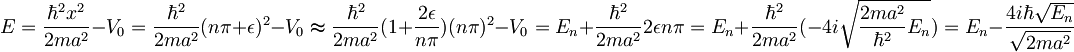
$E=\frac{\hbar^2x^2}{2ma^2}-V_0=\frac{\hbar^2}{2ma^2}(n\pi+\epsilon)^2-V_0\thickapprox \frac{\hbar^2}{2ma^2}(1+\frac{2\epsilon}{n\pi})(n\pi)^2-V_0=E_n+\frac{\hbar^2}{2ma^2}2\epsilon n\pi=E_n+\frac{\hbar^2}{2ma^2}(-4i\sqrt{\frac{2ma^2}{\hbar^2}E_n})=E_n-\frac{4i\hbar\sqrt{E_n}}{\sqrt{2ma^2}}$

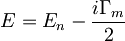
$E=E_n-\frac{i\Gamma_m}{2}$

Iščemo, kako sta povezana razpadni čas kvazivezanega stanja in širina ustrezne resonance. Naredimo časovni razvoj valovne funkcije:

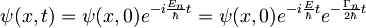
$\psi(x,t)=\psi(x,0)e^{-i\frac{E_n}{\hbar}t}=\psi(x,0)e^{-i\frac{E}{\hbar}t}e^{-\frac{\Gamma_n}{2\hbar}t}$

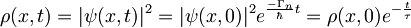
$\rho(x,t)=|\psi(x,t)|^2=|\psi(x,0)|^2e^{\frac{-\Gamma_n}{\hbar}t}=\rho(x,0)e^{-\frac{t}{\tau}}$

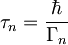
$\tau_n=\frac{\hbar}{\Gamma_n}$

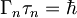
$\Gamma_n \tau_n=\hbar$

$τ$ - širina resonance

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Kvazivezana_stanja_kon%C4%8Dne_potencialne_jame«

 Pri eni izmed prejšnjih vaj smo prišli do izraza za prepustnost končne potencialne jame:
-<math>T=|t|^2=\bigg(\frac{e^{-ik_3a}}{cosk_2a-\frac{i}{2}(\frac{k_2}{k_3}+\frac{k_3}{k_2})sink_2a}\bigg)^2</math>
+<math>T=|t|^2=\bigg|\frac{e^{-ik_3a}}{cosk_2a-\frac{i}{2}(\frac{k_2}{k_3}+\frac{k_3}{k_2})sink_2a}\bigg|^2</math>
 in v bližini resonanc:
-<math>T=|t|^2=\bigg(\frac{(-1)^ne^{-ik_3a}}{E-E_n+i\frac{\Gamma}{2}}\bigg)^2</math>
+<math>T=|t|^2=\bigg|\frac{(-1)^ne^{-ik_3a}}{E-E_n+i\frac{\Gamma}{2}}\bigg|^2</math>
 ----
 ----
-Iščemo, kako sta povezana razpadni čas kvazivezanega stanja in širina ustrezne resonance. Naredimo časovni razvoj:
+Iščemo, kako sta povezana razpadni čas kvazivezanega stanja in širina ustrezne resonance. Naredimo časovni razvoj valovne funkcije:
 <math>\psi(x,t)=\psi(x,0)e^{-i\frac{E_n}{\hbar}t}=\psi(x,0)e^{-i\frac{E}{\hbar}t}e^{-\frac{\Gamma_n}{2\hbar}t}</math>