Časovno odvisna perturbacija II
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 17:11, 1 junij 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == Obravnavaj sistem dveh delcev s spinom <math>1/2</math> s hamiltonianom <math>H=\begin{cases}0,&t\leq 0\\\frac{4\Delta}{\hbar^2}\mathbf{S}_1\cdot\mathbf{S}_2,&t>0\end{cases}...) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (00:31, 21 september 2007) (spremeni) (undo) Zigalenarcic (Pogovor | prispevki) |
||
| Vrstica 10: | Vrstica 10: | ||
| Pod katerimi pogoji da perturbacijska teorija pravilen rezultat? | Pod katerimi pogoji da perturbacijska teorija pravilen rezultat? | ||
| - | == Rešitev == | + | == [[Media:Casovna2.pdf|Rešitev]] == |
Trenutna redakcija
[spremeni] Naloga
Obravnavaj sistem dveh delcev s spinom 1 / 2 s hamiltonianom
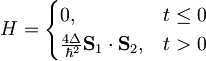
Sistem je za 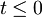 v stanju
v stanju 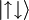 . Pošči verjetnost, da se sistem ob času t > 0 nahaja v stanju
. Pošči verjetnost, da se sistem ob času t > 0 nahaja v stanju 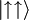 ,
, 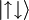 ,
, 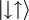 ali
ali 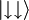
- če problem rešiš točno.
- v prvem redu perturbacije.
Pod katerimi pogoji da perturbacijska teorija pravilen rezultat?