Dvodimenzionalni harmonski oscilator
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 16:08, 24 maj 2007 (spremeni) 193.77.91.65 (Pogovor) (test) ← Pojdi na prejšnje urejanje |
Redakcija: 16:09, 24 maj 2007 (spremeni) (undo) 193.77.91.65 (Pogovor) (Replacing page with '== Naloga == Obravnavaj lastna stanja dvodimenzionalnega harmonskega oscilatorja <math>H=\frac{\mathbf{p^2}}{2m}+\frac{1}{2}a_x x^2+\frac{1}{2}a_y y^2 </math>. V primeru, ...') Novejše urejanje → |
||
| Vrstica 10: | Vrstica 10: | ||
| == Rešitev == | == Rešitev == | ||
| - | |||
| - | |||
| - | \subsubsection{\textbf{Naloga:}\ } | ||
| - | |||
| - | Obravnavaj Lastna stanja dvodimenzionalnega harmonskega oscilatorja. | ||
| - | |||
| - | \[ | ||
| - | H=\frac{\mathbf{p}^{2}}{2m}+\frac{1}{2}a_{x}x^{2}+\frac{1}{2}a_{y}y^{2} | ||
| - | \] | ||
| - | |||
| - | V primeru ko je $a_{x}=\allowbreak a_{y}$ poi\v{s}\v{c}i taka lastna stanja, | ||
| - | ki so hkrati tudi lastna stanja operatorja vrtilne koli\v{c}ine okoli osi | ||
| - | z:\ | ||
| - | \[ | ||
| - | L_{z}=-i\hbar \frac{\partial }{\partial z} | ||
| - | \] | ||
| - | |||
| - | \subsubsection{\protect\bigskip Lastna stanja vsote neodvisnih Hamiltonovih | ||
| - | operatorjev} | ||
| - | |||
| - | V splo\v{s}nem velja, da \v{c}e lahko hamiltonian razbijemo na vsoto | ||
| - | neodvisnih \v{c}lenov $H_{i}$, je lastna funkcija takega hamiltoniana oblike% | ||
| - | \[ | ||
| - | \psi =\prod\limits_{i=1}^{n}\psi _{i} | ||
| - | \]% | ||
| - | kjer je $\psi _{i}$ lastna funkcija operatorja $H_{i}$, lastna vrednost pa | ||
| - | je vsota lastnih vrednosti za posamezne $H_{i}$. To vidimo iz% | ||
| - | \[ | ||
| - | \left( H_{1}+H_{2}+...+H_{n}\right) \psi _{1}\psi _{2}...\psi | ||
| - | _{n}=(E_{1}+E_{2}+...+E_{n})\psi _{1}\psi _{2}...\psi _{n} | ||
| - | \]% | ||
| - | \[ | ||
| - | H_{1}\psi _{1}\psi _{2}...\psi _{n}+H_{2}\psi _{1}\psi _{2}...\psi | ||
| - | _{n}+...+H_{n}\psi _{1}\psi _{2}...\psi _{n}=E_{1}\psi _{1}\psi _{2}...\psi | ||
| - | _{n}+E_{2}\psi _{1}\psi _{2}...\psi _{n}+...+E_{n}\psi _{1}\psi _{2}...\psi | ||
| - | _{n} | ||
| - | \]% | ||
| - | Vidimo, da je $H_{i}\psi _{1}\psi _{2}...\psi _{i}...\psi _{n}=E_{i}\psi | ||
| - | _{1}\psi _{2}...\psi _{i}...\psi _{n}$, saj operator $H_{i}$ deluje le na | ||
| - | funkcijo $\psi _{i}$, vse ostale pa se iz izraza okraj\v{s}ajo. | ||
| - | |||
| - | \subsubsection{\protect\bigskip Lastna stanja 2D harmoni\v{c}nega oscilatorja% | ||
| - | } | ||
| - | |||
| - | Hamiltonian za 2D harmoni\v{c}ni oscilator zapi\v{s}emo v komponentah:% | ||
| - | \[ | ||
| - | H=\frac{p_{x}^{2}}{2m}+\frac{p_{y}^{2}}{2m}+\frac{1}{2}a_{x}x^{2}+\frac{1}{2}% | ||
| - | a_{y}y^{2}=H_{x}+H_{y} | ||
| - | \]% | ||
| - | Vidimo, da ga lahko razstavimo v vsoto hamiltonianov za posamezna | ||
| - | oscilatorja, torej bo lastno stanje enako produktu lastnih stanj | ||
| - | hamiltonovega operatorja za posamezno smer. | ||
| - | |||
| - | Najprej si poglejmo poseben primer: | ||
| - | |||
| - | \paragraph{$a_{x}=0,a_{y}>0$} | ||
| - | |||
| - | V smeri x torej nimamo vezanega stanja, re\v{s}itev predstavlja ravni val% | ||
| - | \[ | ||
| - | \psi _{x}=e^{ik_{x}x}={}_{x}\langle x|k_{x}\rangle _{x} | ||
| - | \]% | ||
| - | kjer je $k_{x}=\frac{1}{\hbar }\sqrt{2mE_{x}}$, v smeri y pa imamo% | ||
| - | \[ | ||
| - | \psi _{y}={}_{y}\langle y|n_{y}\rangle _{y} | ||
| - | \]% | ||
| - | kjer je $|n_{y}\rangle _{y}=\frac{a_{y}^{+n}}{\sqrt{n!}}|0\rangle _{y}$ n-to | ||
| - | lastno stanje enodimenzionalnega harmoni\v{c}nega oscilatorja. Celotna | ||
| - | valovna funkcija je torej produkt, ki ga ozna\v{c}imo:% | ||
| - | \[ | ||
| - | |k_{x}n_{y}\rangle =|k_{x}\rangle |n_{y}\rangle , | ||
| - | \]% | ||
| - | lastno energijo pa zapi\v{s}emo kot% | ||
| - | \[ | ||
| - | E=E_{x}+E_{y}=\frac{(\hbar k_{x})^{2}}{2m}+\hbar \omega _{y}\left( n_{y}+% | ||
| - | \frac{1}{2}\right) | ||
| - | \]% | ||
| - | kjer je $\omega _{y}=\sqrt{\frac{a_{y}}{m}}.$ | ||
| - | |||
| - | \paragraph{$a_{x}>0,a_{y}>0$} | ||
| - | |||
| - | V tem primeru imamo prava vezana stanja, ki jih zapi\v{s}emo kot% | ||
| - | \[ | ||
| - | |n_{x}n_{y}\rangle =|n_{x}\rangle _{x}|n_{y}\rangle _{y} | ||
| - | \]% | ||
| - | z lastno energijo | ||
| - | \[ | ||
| - | E=\hbar \omega _{x}\left( n_{x}+\frac{1}{2}\right) +\hbar \omega _{y}\left( | ||
| - | n_{y}+\frac{1}{2}\right) | ||
| - | \] | ||
| - | |||
| - | \paragraph{$\protect\bigskip a_{x}=a_{y}=a$} | ||
| - | |||
| - | V primeru, da imamo $a_{x}=a_{y}=a$, ima potencial rotacijsko simetri\v{c}en | ||
| - | paraboli\v{c}nen profil. Lastne energije so v tem primeru enake% | ||
| - | \[ | ||
| - | E=\hbar \omega (n_{x}+n_{y}+1) | ||
| - | \]% | ||
| - | kjer je $\omega =\sqrt{\frac{a}{m}}$. Vidimo, da dobimo stanja, ki so | ||
| - | degenerirana: | ||
| - | |||
| - | \[ | ||
| - | \begin{tabular}{ll} | ||
| - | $n_{x}$ & $n_{y}$ \\ \hline | ||
| - | \multicolumn{1}{|l}{$0$} & \multicolumn{1}{l|}{$0$} \\ \hline | ||
| - | \multicolumn{1}{|l}{$0$} & \multicolumn{1}{l|}{$1$} \\ | ||
| - | \multicolumn{1}{|l}{$1$} & \multicolumn{1}{l|}{$0$} \\ \hline | ||
| - | \multicolumn{1}{|l}{$2$} & \multicolumn{1}{l|}{$0$} \\ | ||
| - | \multicolumn{1}{|l}{$1$} & \multicolumn{1}{l|}{$1$} \\ | ||
| - | \multicolumn{1}{|l}{$0$} & \multicolumn{1}{l|}{$1$} \\ \hline | ||
| - | \end{tabular}% | ||
| - | \] | ||
| - | |||
| - | $n$ - to stanje je torej $(n+1)$ krat degenerirano. | ||
| - | |||
| - | \subsubsection{Lastna stanja operatorja vrtilne koli\v{c}ine} | ||
| - | |||
| - | Zgornji hamiltonian zapi\v{s}emo eksplicitno v polarnem koordinatnem | ||
| - | sistemu: | ||
| - | \[ | ||
| - | H\ =-\frac{\hbar ^{2}}{2m}\nabla ^{2}+\frac{1}{2}a\left( x^{2}+y^{2}\right) | ||
| - | =-\frac{\hbar ^{2}}{2m}\left[ \frac{1}{r}\frac{\partial }{\partial r}\left( r% | ||
| - | \frac{\partial }{\partial r}\right) +\frac{1}{r^{2}}\frac{\partial ^{2}}{% | ||
| - | \partial \varphi ^{2}}\right] +\frac{1}{2}ar^{2} | ||
| - | \]% | ||
| - | Vidimo, da komponenta $\varphi $ v izrazu ne nastopa eksplicitno. \v{C}e zapi% | ||
| - | \v{s}emo operator vrtilne koli\v{c}ine% | ||
| - | \[ | ||
| - | L_{z}=-i\hbar \frac{\partial }{\partial \varphi }, | ||
| - | \]% | ||
| - | vidimo, da velja: $\left[ L_{z},H\right] =0$, torej je lastna vrednost | ||
| - | operatorja $L_{z}$ dobro kvantno \v{s}tevilo. Lastna stanja vrtilne koli\v{c}% | ||
| - | ine dobimo:% | ||
| - | \[ | ||
| - | L_{z}|\psi \rangle =l|\psi \rangle | ||
| - | \]% | ||
| - | \[ | ||
| - | -i\hbar \frac{\partial \psi }{\partial \varphi }=l\psi | ||
| - | \]% | ||
| - | \[ | ||
| - | \psi =Ae^{i\frac{l}{\hbar }\varphi } | ||
| - | \] | ||
| - | |||
| - | Upo\v{s}tevamo periodi\v{c}ni robni pogoj: | ||
| - | \[ | ||
| - | \psi \left( 2\pi +\varphi \right) =\psi \left( \varphi \right) | ||
| - | \]% | ||
| - | \[ | ||
| - | e^{i\frac{l}{\hbar }2\pi }=1\Rightarrow \frac{l}{\hbar }2\pi =2\pi | ||
| - | m\Rightarrow l=m\hbar | ||
| - | \] | ||
| - | |||
| - | Izraz \v{s}e normaliziramo:% | ||
| - | \[ | ||
| - | 1=\int_{0}^{2\pi }\psi ^{\ast }\psi d\varphi =A^{2}2\pi \Rightarrow A=\frac{1% | ||
| - | }{\sqrt{2\pi }} | ||
| - | \]% | ||
| - | Valovna funkcija je torej% | ||
| - | \[ | ||
| - | \psi _{m}\left( \varphi \right) =\frac{1}{\sqrt{2\pi }}e^{im\varphi } | ||
| - | \]% | ||
| - | Ker sta torej $n=n_{1}+n_{2}$ in $m$ dobri kvantni \v{s}tevili, lahko iz teh | ||
| - | stanj sestavimo bazo. Poglejmo sedaj, kako izrazimo bazne vektorje te nove | ||
| - | baze $|nm\rangle $ z baznimi vektorji stare baze $|n_{1}n_{2}\rangle .$ | ||
| - | |||
| - | Prvi dve stanji enodimenzionalnega harmoni\v{c}nega oscilatorja poznamo:% | ||
| - | \[ | ||
| - | \psi _{0}(x)=\frac{1}{\sqrt[4]{\pi x_{0}^{2}}}e^{-\frac{x^{2}}{2x_{0}^{2}}} | ||
| - | \]% | ||
| - | \[ | ||
| - | \psi _{1}(x)=\frac{\sqrt{2}x}{x_{0}}\psi _{0}(x) | ||
| - | \]% | ||
| - | Oglejmo si torej stanja $|1,0\rangle ,$ $|0,1\rangle $, (v bazi $% | ||
| - | |n_{1}n_{2}\rangle $) in jih posku\v{s}ajmo kombinirati tako, da bomo lahko | ||
| - | iz njih dobili lastna stanja v bazi $|nm\rangle ,$ ki bodo hkrati lastna | ||
| - | stanja $H$ in $L_{z}.$% | ||
| - | \[ | ||
| - | \psi _{01}=\psi _{0}\psi _{1}=\frac{1}{\sqrt[4]{\pi x_{0}^{2}}}e^{-\frac{% | ||
| - | x^{2}}{2x_{0}^{2}}}\sqrt{2}\frac{y}{x_{0}}\frac{1}{\sqrt[4]{\pi x_{0}^{2}}}% | ||
| - | e^{-\frac{y^{2}}{2x_{0}^{2}}}=\sqrt{\frac{2}{\pi }}\frac{1}{x_{0}^{2}}r\sin | ||
| - | \varphi \text{ }e^{-\frac{r^{2}}{2x_{0}^{2}}} | ||
| - | \]% | ||
| - | \[ | ||
| - | \psi _{10}=\psi _{1}\psi _{0}=\sqrt{\frac{2}{\pi }}\frac{1}{x_{0}^{2}}r\cos | ||
| - | \varphi \text{ }e^{-\frac{r^{2}}{2x_{0}^{2}}} | ||
| - | \]% | ||
| - | kjer smo upo\v{s}tevali polarni zapis:\ $x=r\cos \varphi $ in $y=r\sin | ||
| - | \varphi .$\ Vidimo, da lahko valovni funkciji sestavimo tako, da iz kotnih | ||
| - | funkcij dobimo ravno \v{c}len $e^{im\varphi }$, kjer je $m$ lahko 1 ali -1.% | ||
| - | \[ | ||
| - | |1,\pm 1\rangle _{nm}=\frac{1}{\sqrt{2}}\left( |1,0\rangle _{n_{1}n_{2}}\pm | ||
| - | i|0,1\rangle _{n_{1}n_{2}}\right) | ||
| - | \]% | ||
| - | Poleg valovne funkcije smo zapisali oznako baze. | ||
| - | |||
| - | Ta postopek je bil trivialen za prvo vzbujeno stanje, za vi\v{s}ja stanja pa | ||
| - | ni mogo\v{c}e tako enostavno ugotoviti, zato bomo izra\v{c}un ponovili z | ||
| - | nekoliko bolj splo\v{s}nim postopkom. V splo\v{s}nem za lastna stanja | ||
| - | vrtilne koli\v{c}ine velja% | ||
| - | \[ | ||
| - | L_{z}\psi =l\psi | ||
| - | \]% | ||
| - | kjer je $l=m\hbar $. Zapi\v{s}emo splo\v{s}en nastavek za valovno funkcijo v | ||
| - | stari bazi:% | ||
| - | \[ | ||
| - | \psi =a|1,0\rangle +b|0,1\rangle | ||
| - | \]% | ||
| - | V nastavek smo vklju\v{c}ili zgolj stanja z isto energijo. Ta nastavek | ||
| - | vstavimo v ena\v{c}bo za lastna stanja vrtilne koli\v{c}ine in dobimo% | ||
| - | \[ | ||
| - | aL_{z}|1,0\rangle +bL_{z}|0,1\rangle =am\hbar |1,0\rangle +bm\hbar | ||
| - | |0,1\rangle | ||
| - | \]% | ||
| - | \v{C}e sedaj ena\v{c}bo posami\v{c} z desne mno\v{z}imo z $\langle 1,0|$ in $% | ||
| - | \langle 0,1|$ (oz. projeciramo ena\v{c}bo na posamezne smeri), dobimo ena% | ||
| - | \v{c}bi: | ||
| - | \[ | ||
| - | \langle 1,0|L_{z}|1,0\rangle a+\langle 1,0|L_{z}|0,1\rangle b=am\hbar | ||
| - | \]% | ||
| - | \[ | ||
| - | \langle 0,1|L_{z}|1,0\rangle a+\langle 0,1|L_{z}|0,1\rangle b=bm\hbar | ||
| - | \]% | ||
| - | Oziroma v matri\v{c}ni obliki:% | ||
| - | \[ | ||
| - | \begin{bmatrix} | ||
| - | \langle 1,0|L_{z}|1,0\rangle & \langle 1,0|L_{z}|0,1\rangle \\ | ||
| - | \langle 0,1|L_{z}|1,0\rangle & \langle 0,1|L_{z}|0,1\rangle | ||
| - | \end{bmatrix}% | ||
| - | \begin{bmatrix} | ||
| - | a \\ | ||
| - | b% | ||
| - | \end{bmatrix}% | ||
| - | =m\hbar | ||
| - | \begin{bmatrix} | ||
| - | a \\ | ||
| - | b% | ||
| - | \end{bmatrix}% | ||
| - | \]% | ||
| - | Vidimo torej, da ima ta matrika lastni vrednosti, ki sta ravno lastni | ||
| - | vrednosti operatorja vrtilne koli\v{c}ine, in lastna vektorja, ki sta ravno | ||
| - | koeficienta razvoja valovne funkcije po novi bazi.\ Lastni vrednosti matrike | ||
| - | nam bosta torej definirali nova bazna vektorja, pripadajo\v{c}a lastna | ||
| - | vektorja pa bosta koeficienta razvoja teh novih baznih vektorjev po stari | ||
| - | bazi. V na\v{s}em primeru torej dobimo:% | ||
| - | \[ | ||
| - | \langle 0,1|L_{z}|0,1\rangle =\int\limits_{0}^{2\pi }\frac{2}{\pi }\frac{1}{% | ||
| - | x_{0}^{2}}r^{2}\sin \varphi \text{ }\left( -i\hbar \right) \cos \varphi | ||
| - | \text{ }e^{-\frac{2r^{2}}{2x_{0}^{2}}}rdrd\varphi =0\text{, \ \ \ \ integral | ||
| - | kotnega dela je o\v{c}itno ni\v{c}} | ||
| - | \]% | ||
| - | \[ | ||
| - | \langle 1,0|L_{z}|1,0\rangle =\int_{0}^{2\pi }\frac{2}{\pi }\frac{1}{% | ||
| - | x_{0}^{2}}r^{2}\cos \varphi \text{ }\left( i\hbar \right) \sin \varphi \text{ | ||
| - | }e^{-\frac{2r^{2}}{2x_{0}^{2}}}rdrd\varphi =0 | ||
| - | \]% | ||
| - | \[ | ||
| - | \langle 0,1|L_{z}|1,0\rangle =\int\limits_{0}^{2\pi }\frac{2}{\pi }\frac{1}{% | ||
| - | x_{0}^{4}}r^{2}\sin \varphi \left( -i\hbar \right) \left( -\sin \varphi | ||
| - | \right) e^{\frac{-2r^{2}}{2x_{0}^{2}}}rdrd\varphi =i\hbar | ||
| - | \int\limits_{0}^{2\pi }|\psi _{01}|^{2}=i\hbar | ||
| - | \]% | ||
| - | \[ | ||
| - | \langle 1,0|L_{z}|0,1\rangle =\int\limits_{0}^{2\pi }\frac{2}{\pi }\frac{1}{% | ||
| - | x_{0}^{4}}r^{2}\cos \varphi \left( -i\hbar \right) \left( \cos \varphi | ||
| - | \right) e^{\frac{-2r^{2}}{2x_{0}^{2}}}rdrd\varphi =-i\hbar | ||
| - | \int\limits_{0}^{2\pi }|\psi _{10}|^{2}=-i\hbar | ||
| - | \] | ||
| - | |||
| - | Imamo torej matriko: | ||
| - | \[ | ||
| - | \begin{bmatrix} | ||
| - | 0 & i\hbar \\ | ||
| - | -i\hbar & 0% | ||
| - | \end{bmatrix}% | ||
| - | \]% | ||
| - | Lastni vrednosti sta: | ||
| - | \[ | ||
| - | \lambda ^{2}-\hbar ^{2}=0\Rightarrow \lambda _{1,2}=\pm \hbar | ||
| - | \]% | ||
| - | Lastna vektorja pa:% | ||
| - | \[ | ||
| - | c% | ||
| - | \begin{bmatrix} | ||
| - | 1 \\ | ||
| - | i% | ||
| - | \end{bmatrix}% | ||
| - | ,\text{ \ \ }c% | ||
| - | \begin{bmatrix} | ||
| - | 1 \\ | ||
| - | -i% | ||
| - | \end{bmatrix}% | ||
| - | ,\text{ }c=\frac{1}{\sqrt{2}}\text{ (dobimo iz normalizacije)} | ||
| - | \]% | ||
| - | Kon\v{c}ni rezultat je torej: | ||
| - | |||
| - | \[ | ||
| - | |1,1\rangle =\frac{1}{\sqrt{2}}\left( |1,0\rangle +i|0,1\rangle \right) | ||
| - | \]% | ||
| - | \[ | ||
| - | |1,-1\rangle =\frac{1}{\sqrt{2}}\left( |1,0\rangle -i|0,1\rangle \right) | ||
| - | \]% | ||
| - | kar je isto kot prej. Enako bi lahko postopali tudi za vi\v{s}ja vzbujena | ||
| - | stanja. | ||
| - | |||
| - | \end{document} | ||
Redakcija: 16:09, 24 maj 2007
Naloga
Obravnavaj lastna stanja dvodimenzionalnega harmonskega oscilatorja
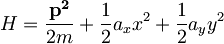 .
.
V primeru, ko je ax = ay, poišči taka lastna stanja, ki so hkrati tudi lastna stanja operatorja vrtilne količine okoli osi z
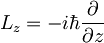 .
.