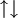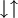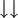Spin II
Iz Kvantna Mehanika I 2006 - 2007
| Redakcija: 08:26, 12 maj 2007 (spremeni) 84.41.82.164 (Pogovor) (003) ← Pojdi na prejšnje urejanje |
Redakcija: 09:06, 12 maj 2007 (spremeni) (undo) 84.41.82.164 (Pogovor) (004) Novejše urejanje → |
||
| Vrstica 13: | Vrstica 13: | ||
| == Rešitev == | == Rešitev == | ||
| - | Najprej je treba poiskati začetno valovno funkcijo <math> \vert \psi \rangle </math> obeh delcev. Začetna pogoja nam povesta, da ob <math> t = 0 </math> prvi spin kaže v smer <math> x </math>, drugi pa v smer <math> y </math>. Os <math> z </math> naj bo glavna, kot je navada. To pomeni, da se bosta stanji <math> \vert \uparrow \rangle </math> | + | ==Začetna valovna funkcija== |
| + | |||
| + | Najprej je treba poiskati začetno valovno funkcijo <math> \vert \psi \rangle </math> obeh delcev. Začetna pogoja nam povesta, da ob <math> t = 0 </math> prvi spin kaže v smer <math> x </math>, drugi pa v smer <math> y </math>. Os <math> z </math> naj bo glavna, kot je navada. To pomeni, da se bosta stanji <math> \vert \uparrow \rangle </math> in <math> \vert \downarrow \rangle </math> nanašali na os <math> z </math>. | ||
| + | |||
| + | ===Baza sistema=== | ||
| + | Da lahko zapišemo poljubno stanje sistema dveh delcev s spinom <math> 1/2 </math>, moramo najprej ugotoviti bazo le tega. Privzamemo, da spina med seboj ne interagirata, torej da sta neodvisna. Vsak spin je lahko v stanju <math> \vert \uparrow \rangle </math> in <math> ali <math> \vert \downarrow \rangle </math> in <math>. Če na oba spina gledamo kot na celoto ugotovimo, da imamo štiri možna <bf> produktna stanja </bf>: | ||
| + | |||
| + | # <math> \uparrow \uparrow </math> | ||
| + | # <math> \uparrow \downarrow </math> | ||
| + | # <math> \downarrow \uparrow </math> | ||
| + | # <math> \downarrow \downarrow </math> | ||
Redakcija: 09:06, 12 maj 2007
Vsebina |
Naloga
Za sistem dveh delcev s spinom 1 / 2 velja
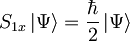
in
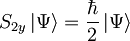 .
.
Kolikšna je verjetnost, da ob meritvi velikosti celotnega spina sistema delcev izmerimo vrednost 0?
Rešitev
Začetna valovna funkcija
Najprej je treba poiskati začetno valovno funkcijo 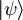 obeh delcev. Začetna pogoja nam povesta, da ob t = 0 prvi spin kaže v smer x, drugi pa v smer y. Os z naj bo glavna, kot je navada. To pomeni, da se bosta stanji
obeh delcev. Začetna pogoja nam povesta, da ob t = 0 prvi spin kaže v smer x, drugi pa v smer y. Os z naj bo glavna, kot je navada. To pomeni, da se bosta stanji 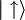 in
in 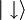 nanašali na os z.
nanašali na os z.
Baza sistema
Da lahko zapišemo poljubno stanje sistema dveh delcev s spinom 1 / 2, moramo najprej ugotoviti bazo le tega. Privzamemo, da spina med seboj ne interagirata, torej da sta neodvisna. Vsak spin je lahko v stanju 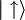 in
in 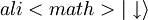 in Ni mi uspelo razčleniti (Začasne mape za matematiko ne morem ustvariti ali pisati vanjo.): . Če na oba spina gledamo kot na celoto ugotovimo, da imamo štiri možna <bf> produktna stanja </bf>: # <math> \uparrow \uparrow
in Ni mi uspelo razčleniti (Začasne mape za matematiko ne morem ustvariti ali pisati vanjo.): . Če na oba spina gledamo kot na celoto ugotovimo, da imamo štiri možna <bf> produktna stanja </bf>: # <math> \uparrow \uparrow