Začnimo z zapisom Schrödingerjeve enačbe v brezdimenzijski obliki. Smisel tega početja je eliminacija nepotrebnih parametrov v sistemu - kar se izkaže tudi v tem primeru.
Zapišimo Schrödingerjevo enačbo v vsej dimenzijski lepoti:

Poiskati moramo primerne skalirne faktorje za količine x ter E. Pogledamo kakšno enoto ima količina ter . Iz teh količin lahko "skuhamo" faktorja z enotama meter in joule:

Vedeti moramo še, kako se izrazi delta funkcija z brezdimenzijsko dolžino. Velja:

Nove količine nato vtaknemo v Schrödingerjevo enačbo:

Ugotovimo, da je možno člen izraziti kot , to vstavimo v enačbo, zamenjamo oznake s črtico s takimi brez črtice (zaradi lažje pisave) in pokrajšamo člen . Dobimo:

Vidimo, da je enačba zares odvisna samo od parametrov ter in ne od treh parametrov . Sedaj se lotimo reševanja te enačbe s standardnimi postopki. Najprej napišemo valovne funkcije v vseh treh območjih. V vseh območjih dopustimo samo eksponentno padajoče rešitve, kajti potencial je 0 za vse x, razen za dve točki (a in -a od izhodišča).

Poznamo še nekaj dodatnih pogojev:
    1. = , ker mora biti valovna funkcija povsod zvezna
    2. isto za par in
    3. in podobno še za drugo delta funkcijo
Pogoji nam dajo sistem štirih lin. enačb za neznanke C1 do C4. Zapišimo jih v obliki matrike, iz pogoja, da mora biti determinanta nič, pa bomo dobili pogoje za obstoj vezanih stanj.

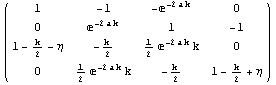
Vezana stanja so karakterizirana z energijami, manjšimi od 0, zato lahko poiščemo vrednosti parametrov a in η za stanja z energijo 0. Na eni strani krivulje v ravnini a/η se bodo nahajala vezana stanja, na drugi strani pa prosta stanja. Kot smo že ugotovili, mora biti determinanta sistema enaka nič, težava pa  je, da ima ta determinanta vedno ničlo pri k=0 (za vsak a in η). Zato bomo poiskali ničlo drugega reda prek odvoda determinane po k in narisali graf, ki ločuje vezana in prosta stanja.

Nato narišimo še graf energij vezanih stanj v tem problemu. Na zgornjem grafu ni mogoče opaziti, da ponekod obstajata dve različni vezani stanji; zgornji graf namreč prikazuje mejo za obstoj enega vezanega stanja, drugo pa obstaja v vsakem primeru. To je mogoče videti, če si narišemo graf vrednosti determinante od parametrov, ki pa je zaradi berljivosti izpuščen. Zato pojdimo kar k zadnjemu grafu, ki ga sestavimo iz grafa energije prvega in drugega vezanega stanja. Sestavljen graf je prikazan zadnji, pred njim pa sta grafa energije za obe komponenti. Na vrhnjem grafu vidimo, da vezano stanje izgine (energija postane enaka nič), rob teba območja pa podaja ravno narisani graf.

Created by Mathematica  (April 17, 2005)