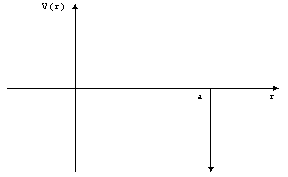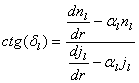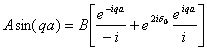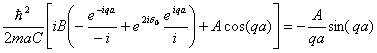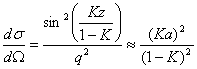|
|
SIPANJE V 3D I
Martin Gorjan |
|
1.
NALOGA: Delec se
sipa na krogelno simetričnem potencialu ![]() .
.
a) Najmanj kolikšen mora biti C, da obstaja vezano stanje?
b) Izračunaj diferencialni in totalni sipalni presek, če ima sipani delec nizko vpadno hitrost.
|
|
|
|
2. VEZANO STANJE:
Pri vajah smo pokazali (Miha Pelko), da za krogelno simetričen primer lahko uporabimo nastavek
|
|
|
2.1 |
ki pripelje do Schrodingerjeve enačbe oblike
|
|
|
2.2 |
Računamo samo za l = 0, zato sta primerna nastavka za obe območji (1 je za r > a in 2 za r > a)
|
|
|
2.3 |
Robni pogoji pa so
|
|
|
2.4 |
pri čemer je prvi pogoj posledica zahteve po končni rešitvi pri r = 0. Iz prvega in drugega pogoja najprej dobimo
|
|
|
2.5 |
Iz tretjega pogoja dobimo enačbo
|
|
|
2.6 |
Z uporabo druge enačbe (2.5) dobimo končno enačbo za vezana stanja
|
|
|
2.7 |
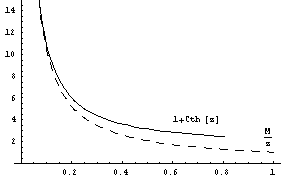
Sedaj iščemo najmanjšo vrednost M, pri kateri še obstaja (pozitivna) rešitev zgornje enačbe. Izkaže se, da je to pri majhni vrednosti spremenljivke z (glej sliko spodaj), zato lahko funkcijo kotangens hiperbolicus razvijemo po Tayloryu.
|
|
|
|
Iz tega dobimo
|
|
|
2.8 |
In ker mora biti z večji od nič, sledi
|
|
|
2.9 |
Končno dobimo rezultat
|
|
|
2.10 |
3. DIFERENCIALNI IN TOTALNI SIPALNI PRESEK:
Pri vajah žal nismo naredili nobene naloge iz sipanja, je pa veliko povedanega v Schwablu (18. poglavje). V splošnem za sipanje na majhni motnji velja:
|
|
|
3.1 |
Zaradi krogelne simetrije funkcije razvijemo po krogelnih funkcijah
|
|
|
3.2 |
Za velike razdalje, kjer je potencial nič, lahko Rl razvijemo po Hanklovih funkcijah
|
|
|
3.3 |
kjer je
|
|
|
3.4 |
in sledi
|
|
|
3.5 |
Za potencial, ki se konča pri a (oz. potencial, ki pada hitreje kot 1/r2), velja
|
|
|
3.6 |
kjer sta jl in nl krogelna Besslova in krogelna Neumannova funkcija. Znak manjše pomeni krogelni del rešitve valovne funkcije za območje, kjer je r < a, če se potencial razteza do a.
Diferencialni in totalni sipalni presek sta definirana kot
|
|
|
3.7 |
Za naš primer (krogelno simetrično, l = 0, počasni delci) velja za diferencialni sipalni presek
|
|
|
3.8 |
Sedaj moramo še izračunati fazni zamike ![]() . Najprej napišemo
ločena nastavka za obe območji: manjše od a in večje od a
. Najprej napišemo
ločena nastavka za obe območji: manjše od a in večje od a
|
|
|
3.9 |
Kjer pomeni j0 ničto krogelno Besselovo funkcijo in h0 obe krogelni Hankelovi funkcij. Z elementarnimi funkcijami se izražajo na sledeč način:
|
|
|
3.10 |
Sedaj uporabimo iste robne pogoje kot v prvem delu naloge (enačbe 2.4), od kjer dobimo iz drugega in tretjega pogoja enačbi
|
|
|
3.11 |
Najprej izločimo normalizacijski konstanti A in B, s tem da enačbi združimo v eno. S precej premetavanja eksponentnih funkcij in njih razvijanja v trigonometrične funkcije dobimo končno
|
|
|
3.12 |
Ker sta obe
spremenljivki z in ![]() dosti manjši od 1, lahko tangensa
razvijemo v Taylorjevo vrsto in dobimo za
dosti manjši od 1, lahko tangensa
razvijemo v Taylorjevo vrsto in dobimo za ![]()
|
|
|
3.13 |
Diferencialni sipalni presek dobimo po enačbi (3.8) in zopet naredimo Taylorjev razvoj
|
|
|
3.14 |
Totalni sipalni presek pa dobimo po enačbi (3.7)
|
|
|
3.15 |