Perturbacija 1

Naloga: Anharmonski oscilator v prvem približku opišemo s potencialom

.

Izračunaj popravke energij lastnih stanj v prvem redu perturbacije. Upoštevaj tudi popravke v drugem redu perturbacije za kubični člen v potencialu.

Rešitev:

Najprej zapišem lastne funkcije harmonskega oscilatorja v splošni obliki:

,

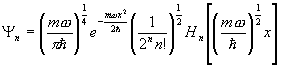kjer so Hn Hermitovi polinomi, definirani z .

Popravek energije v prvem redu perturbacije se izračuna po enačbi .

Pri računanju integrala pa potrebujem še dve pravili za računanje s Hermitovimi polinomi:

  1. Ortogonalnost z utežjo:, če je n=m; v nasprotnem primeru pa je ta skalarni produkt enak nič.
  2. Rekurzijska formula: .

Ko izračunam vse potrebne integrale, dobim rezultat:

,

Če vstavim v enačbo n=0, dobim rezultat , kar se ujema z direktno izračunanim popravkom, ko že na začetku vstavim v integral samo ničto lastno funkcijo.

Ta popravek energije je prispevek člena z x4 v potencialu. Kubični člen v prvem redu perturbacije ne prispeva nič, zato grem računat še drugi red perturbacije, vendar samo za kubični člen v potencialu.

Popravek energije v drugem redu perturbacije je , kjer je .

je energija harmonskega oscilatorja .

Najprej računam matrični element potenciala Vln. Ko lastne funkcije in potencial vstavim v enačbo, primerjam indekse pri Hermitovih polinomih in upoštevam njihovo ortogonalnost. Od nič različne člene za kubični člen v potencialu dobim pri pogojih l=n-3, l=n-1, l=n+1 in l=n+3. V vrsti za drugi popravek energije moram torej sešteti štiri člene.

Zapišimo zdaj te člene:

1.) pri l=n-3: ;

2.) pri l=n-1: ;

3.)pri l=n+1: ;

4.)pri l=n+3: .

Zdaj samo še seštejem te člene in dobim končni rezultat za drugi popravek energije:

.

Celotna energija takega anharmonskega oscilatorja pa je v našem približku:

.