Popravek energije osnovnega stanja vodikovega atoma v šibkem homogenem električnem polju.

Operator energije vodikovega atoma v homogenem električnem polju se zapiše kot

, (1)

.

Zanima nas samo primer, ko je jakost zunanjega električnega polja ( E ) veliko manjša od notranjega električnega polja, zato uporabimo rezultate iz teorije motenj, ki smo jih izpeljali na predavanjih. Energijo stanja zapišemo kot vsoto energije nemotenega stanja (brez zunanjega polja) in popravkov prvega ter drugega reda:

. (2)

Za popravek prvega reda velja enačba:

, (3)

pri čemer je nemoteno stanje. V našem primeru je kar osnovno stanje vodikovega atoma, se pravi

.

Za popravek prvega reda torej dobimo ():

.

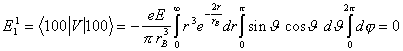Prvi red nam torej ne da popravka, zato moramo upoštevati še drugi red. Pri drugem redu se bomo omejili le na oceno popravka. Za drugi red velja enačba:

. (4)

Če vzamemo le prvi člen v vsoti po n (), dobimo oceno

oziroma

.

Za prvo vzbujeno stanje () so možna kvantna števila , ter . Pri računanju členov nam pomaga dejstvo, da so različni od nič le, če ima funkcija pod integralom sodo parnost ( ). Sferni harmoniki imajo parnost , V ima liho parnost, zato člen v vsoti odpade.

Ostane nam še neenačba

.

Sferni harmoniki so tudi lastne funkcije z-komponente vrtilne količine. Pri računanju členov imamo opraviti z integrali oblike

,

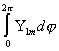ki so različni od nič le, če je m enak nič. Tako dobimo spodnjo mejo absolutne vrednosti popravka drugega reda:

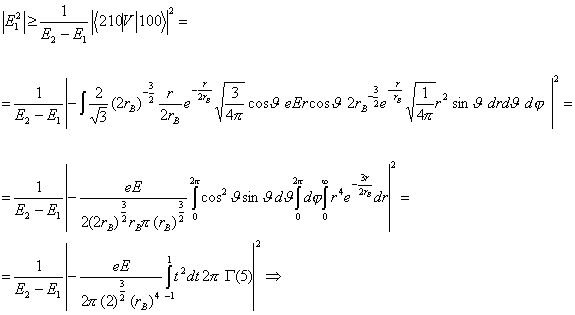
(5)

Ocenimo še zgornjo mejo absolutne vrednosti popravka drugega reda. Vzamemo enačbo (4) in upoštevamo, da velja . Tako dobimo oceno

oziroma

.

V vsoto lahko vključimo tudi člen s kvantnim številom , ker je enak nič. Vsoto lahko zapišemo tudi drugače:

.

Preostane nam le še izračun skalarnega produkta :

Tako dobimo oceno za drugi red popravka v energiji:

. (6)

Izraz lahko še izvrednotimo, če upoštevamo, da je

, , .

Primož Rebernik Ribič