Valovni paket

avtor tipkarije: Borut Levart na zimski vecer 28feb01

---

Elektron je ob casu v stanju z valovno funkcijo

Izracunaj casovni razvoj valovne funkcije, ce se elektron giblje v prostoru, kjer je potencial konstanten. Kako se s casom spreminja verjetnostna gostota?

1. Valovno funkcijo razvijem po lastnih funkcijah Hamiltonovega operatorja, to so ravni valovi .

Lastna vrednost je energija, zatorej velja

V izrazu prepoznam Fourierovo transformacijo. Sledi:

.

2. Elementarni integral se resi tako, da eksponent preoblikujes v popolni kvadrat in vpeljes substitucijo. Bodi vesel, ce dobis:

3. Tretji korak je najpomembnejsi. Valovno funkcijo sedaj lahko zapisem z ravnimi valovi, saj poznam . Razvoj je casoven, zato ostani pozoren:

Ne misli si grdo o meni zaradi naslednje izjave. Zgornji integral je elementaren.  Asistent Matevz za mafijski praktikum bi pripomnil SAFR.
Resno, integral je podoben integralu za , le da je clenov malo vec. Postopas torej po enakem nacinu, kar te privede do casovno krajevnega opisa za elektron. Kakorkoli, toplo ti priporocam, da ga resis na roke.

Verjetnostna gostota

, kjer je


.

4. Cetrti korak je korak, zaradi katerega se je bilo vredno potruditi. Slika. Animacija.

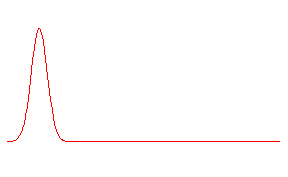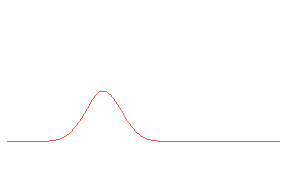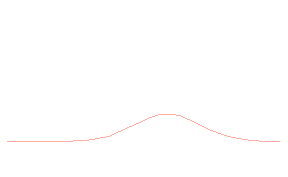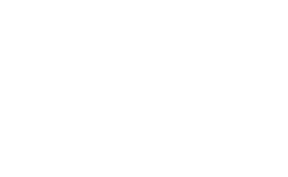
SLIKA: Realni del valovne funkcije elektrona (modra barva) niha in je dolocen z verjetnostno gostoto (rdeca barva).

ANIMACIJA: Valovni paket ali elektron potuje v desno s pricakovano gibalno kolicino. Istocasno postajo verjetnostna gostota vse bolj razmazana in lega nedolocena.

---

Converted by Mathematica