Časovni razvoj valovne funkcije
MATEJ LEBAN, 30. marec 2000
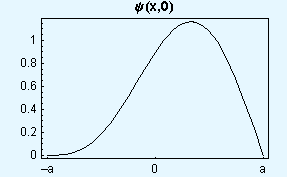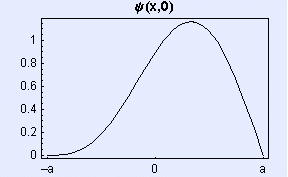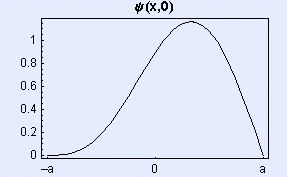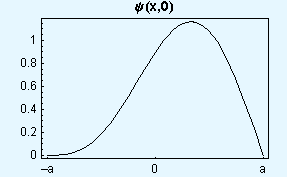
Elektron je ob t = 0 v neskončni potencialni jami širine 2a (med -a in a) z valovno funkcijo:
|
|

|
a) Izračunaj valovno funkcijo elektrona ob poznejših časih.
b) Kako se s časom spreminja verjetnost, da je elektron na desni polovici potencialne jame (x > 0) ?
c) Pokaži, da velja Ehrenfestov teorem za povprečno vrednost gibalne kolicine.
d) Izdelaj simulacijo časovne odvisnosti verjetnostne gostote.
Funkcijo najprej normiram:
![]()
Nastavek:
![]()
kjer so ![]() lastne funkcije za delec v neskončni potencialni jami. Nastavek postavim v Schroedingerjevo enačbo :
lastne funkcije za delec v neskončni potencialni jami. Nastavek postavim v Schroedingerjevo enačbo : ![]() in dobim
in dobim
![]()
![]()
![]()
Za lastne funkcije dobim:
![]()
Dana funkcije je linerarna kombinacija lastnih funkcij:
![]()
Razvita po času pa zgleda takole:
![]()
Verjetnost je enaka:
![]()
Uvedem novo spremenljivko ![]()
![[Graphics:Images/index_gr_14.gif]](Images/index_gr_14.gif)
Verjetnostna gotota:
![[Graphics:Images/index_gr_15.gif]](Images/index_gr_15.gif)
ANIMACIJA: Verjetnostna gostota je simetrična tako v x kakor v t. Verjetnost, da na delec naletimo v desni polovici jame, niha okoli vrednosti 0.5.
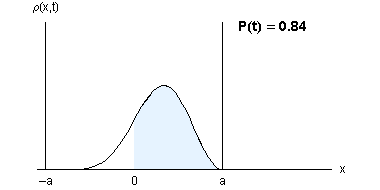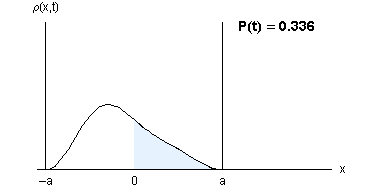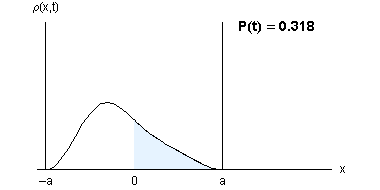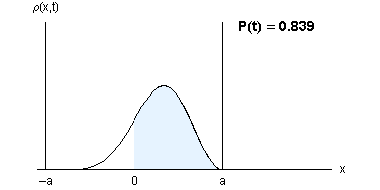
Verjetnost, da je elektron v desni strani potencialne jame:
![]()
1) ![]()
2) ![]()
Pokazati moram da za to valovno funkcijo velja Ehrenfestov teorem
1)
![]()
![]()
Ce <x> odvajam in množim z maso m, vidim da teorem velja.
2)
![]()
![]()
![]()
![]()
![]()